3686. A Simple Tree Problem
Given a rooted tree, each node has a boolean (0 or 1)
labeled on it. Initially, all the labels are 0.
We define this kind of operation: given a subtree,
negate all its labels.
And we want to query the numbers of 1's of a subtree.
Input. Multiple test cases.
First line, two integer n and m, denoting the numbers of nodes and numbers of operations and queries (1 ≤ n ≤ 100000, 1 ≤ m ≤ 10000).
Then a line with n – 1 integers, denoting the parent of node 2..n. Root is node 1.
Then m lines, each line are in
the format "o node" or
"q node", denoting we want
to operate or query on the subtree with root of a certain node.
Output. For each query, output an integer in a line.
Output a blank line after
each test case.
Sample Input
3 2
1 1
o 2
q 1
Sample
Output
1
РЕШЕНИЕ
графы – поиск в глубину – дерево отрезков
Анализ алгоритма
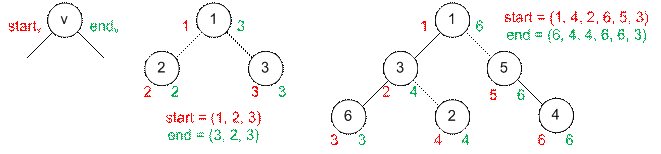
Запустим поиск в глубину из
первой вершины (корня) и в порядке посещения вершин перенумеруем их, например
начиная с 1. Номер i-ой вершины сохраним в start[i]. Рассмотрим поддерево с корнем v. Пусть в результате обхода в глубину все его вершины получили номера от start[v] до cnt.
Заведем еще один массив end и положим end[v]
= cnt. Тогда все вершины поддерева с
корнем v (включая и саму вершину v) имеют номера от start[v] до end[v].
Пусть mas – масив из нулей и единиц, причем mas[i] содержит число, находящееся в i-ой вершине. Построим по нем дерево отрезков. Поскольку изначально во всех
вершинах дерева содержатся 0, то дерево отрезков инициализируем нулями.
Инвертирование значений
всех вершин в поддереве с корнем x
означает инвертирование всех чисел на отрезке [mas[start[v]], mas[end[v]] ]. Соответственно нахождение суммы всех чисел в поддереве с корнем x означает нахождение суммы на отрезке [mas[start[v]],
mas[end[v]] ].
Пример
Реализация алгоритма
#include <cstdio>
#include <vector>
using namespace
std;
int i, n, m, x, u, cnt;
char ch;
vector<vector<int>
> g;
vector<int> start, end;
struct node
{
int summa, add;
};
vector<node> SegTree;
void Push(int
Vertex, int LeftPos, int
Middle, int RightPos)
{
if (SegTree[Vertex].add)
{
SegTree[2*Vertex].add ^= SegTree[Vertex].add;
SegTree[2*Vertex].summa = (Middle - LeftPos + 1) -
SegTree[2*Vertex].summa;
SegTree[2*Vertex+1].add ^= SegTree[Vertex].add;
SegTree[2*Vertex+1].summa = (RightPos - Middle) -
SegTree[2*Vertex+1].summa;
SegTree[Vertex].add
= 0;
}
}
void SwitchValue(int Vertex, int
LeftPos, int RightPos, int
Left, int Right)
{
if (Left > Right) return;
if ((LeftPos == Left) && (RightPos == Right))
{
SegTree[Vertex].add
= 1 - SegTree[Vertex].add;
SegTree[Vertex].summa = (Right - Left + 1) - SegTree[Vertex].summa;
return;
}
int Middle = (LeftPos + RightPos) / 2;
Push(Vertex,LeftPos,Middle,RightPos);
SwitchValue(2*Vertex,
LeftPos, Middle, Left, min(Middle,Right));
SwitchValue(2*Vertex+1, Middle+1, RightPos, max(Left,Middle+1), Right);
SegTree[Vertex].summa
= SegTree[2*Vertex].summa + SegTree[2*Vertex+1].summa;
}
int Summa(int
Vertex, int LeftPos, int
RightPos, int Left, int
Right)
{
if (Left > Right) return
0;
if ((LeftPos == Left) && (RightPos == Right))
return SegTree[Vertex].summa;
int Middle = (LeftPos + RightPos) / 2;
Push(Vertex,LeftPos,Middle,RightPos);
return Summa(2*Vertex, LeftPos, Middle, Left,
min(Middle,Right)) +
Summa(2*Vertex+1,
Middle+1, RightPos, max(Left,Middle+1), Right);
}
void dfs(int
v, int p = -1)
{
start[v] = cnt++;
for(int i = 0; i <
g[v].size(); i++)
{
int to = g[v][i];
if (to != p) dfs(to,v);
}
end[v] = cnt - 1;
}
int main (void)
{
while(scanf("%d
%d",&n,&m) == 2)
{
g.clear();
g.resize(n+1);
for(i = 2; i <= n; i++)
{
scanf("%d",&u);
g[i].push_back(u);
g[u].push_back(i);
}
start.clear();
start.resize(n+1);
end.clear();
end.resize(n+1);
cnt = 1;
dfs(1);
SegTree.clear();
SegTree.resize(4*n+4);
scanf("\n");
for(i = 0; i < m; i++)
{
scanf("%c %d\n",&ch,&x);
if (ch == 'q')
printf("%d\n",Summa(1,1,n,start[x],end[x]));
else
SwitchValue(1,1,n,start[x],end[x]);
}
}
return 0;
}